An Introduction to Binarisation

Tue, Oct 22, 2019

Binarisation is the process of turning a colour or grayscale image into a black and white image. It’s called binarisation as once you’re done, each pixel will either be white (0) or black (1), a binary option. Binarisation is necessary for various types of image analysis, as it makes various image manipulation tasks much more straightforward. OCR is one such process, and all major OCR engines today work on binarised images.

Poor binarisation has been a key cause of poor OCR results for our work, so we have spent some time looking into better solutions to improve our results. We now generally pre-binarise page images before sending them to an OCR engine, which has yielded significant quality improvements to our OCR results. Before we get to that, it’s worth looking in depth at how different binarisation methods work.

Binarisation sounds pretty straightforward, and in the ideal case it is. You can pick a number, and go through each pixel in the image, checking if the pixel is lighter than the number, and if so declaring it to be white, otherwise black.

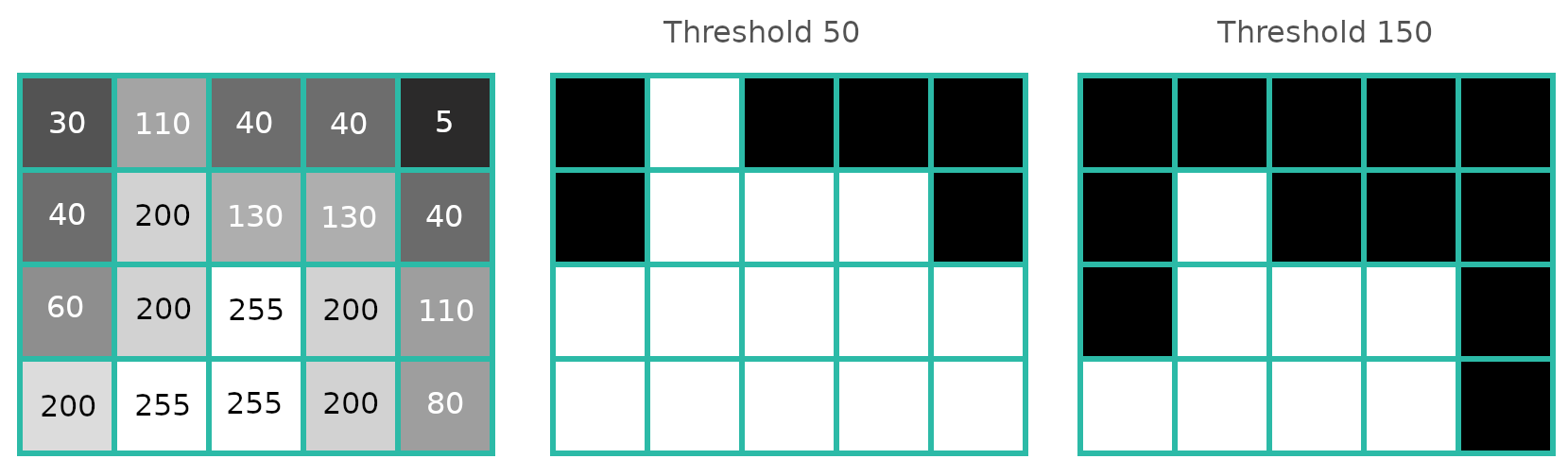
The first issue with this is deciding what number to pick to determine whether a pixel is white or black. This number is called the threshold, and the whole process of binarisation can also called thresholding, as it’s so fundamental to the binarising process. Picking a threshold that is too high will result in too few pixels being marked as black, which in the case of OCR means losing parts of characters, which will make it harder for an OCR engine to correctly recognise text. Picking a threshold that is too low will result in too many pixels being marked as black, which for OCR means that various non-text noise will be included and considered by the OCR engine, again reducing accuracy.

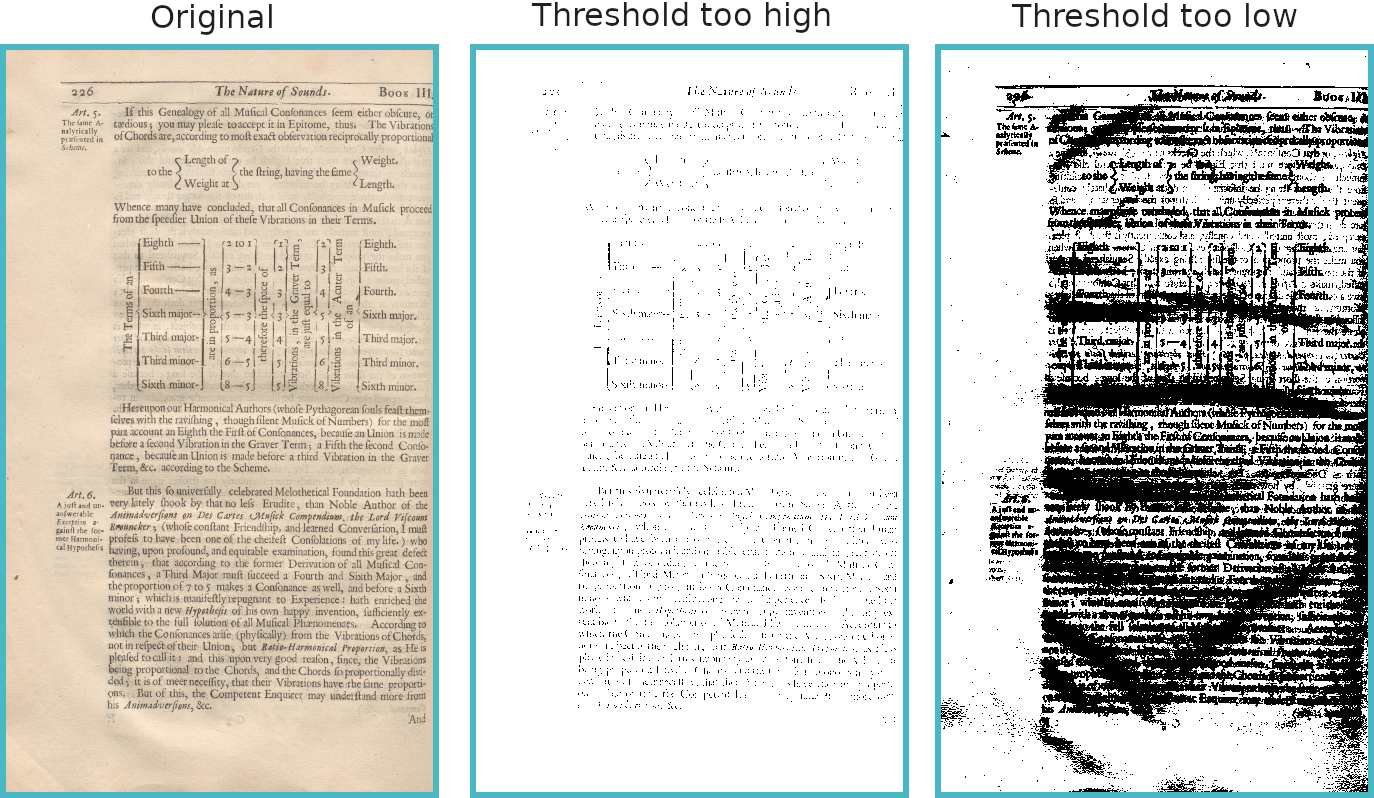
If all page images were printed exactly the same way, and scanned the same way, we could probably get away with just picking an appropriate threshold number for everything. However sadly that is not the case, and the variances can be significantly greater for historical documents.

There are various algorithms to find an appropriate threshold number for a given page. A particularly well-known and commonly used one is called the Otsu algorithm. This works by splitting the pixels in the image into two classes, one for background and one for foreground, with the threshold calculated to minimise the “spread” of both classes. Spread here means how much variation in pixel intensity there is, so by trying to minimise the spread for each class, the threshold aims to find two clusters of similar pixel intensities, one being a common background, the other a common foreground.

Otsu’s algorithm works well for well printed material, on good paper, which has been well scanned, as the brightness of the background and foreground pixels is consistent.

However, even with the most perfectly chosen threshold number, there are certain cases that no global threshold binarisation can do a good job at. Pages which have been scanned with uneven lighting do badly, as the background brightness may be quite different for one corner of a page than another. Global threshold binarisation can also have problems with paper or ink inconsistencies, such as blemishes, splotches or page grain, as they may well have parts which are darker than the global threshold.

Both of these criticisms could be addressed by using an algorithm that could alter the threshold according to the conditions of the region on the page. That will be covered in the next blog post, Adaptive Binarisation.